Deriving the Y Combinator

What is the Y Combinator?

In order to understand the Y combinator, one must first understand recursion. Here's a definition.

recursion (noun)
see "recursion"

Kidding! But nonetheless, this definition captures the essence of recursion: self-reference. In our case — programming — recursion allows for the succint description of a repeating process.

Recursion can be puzzling at first, but oftentimes, it allows us to write code that is closer to the true intent of what we wish to do than an imperative, loopy style. Here are a few examples.

/**
 * Imperative style
 */
function factorialA(x) {
  let result = 1;
  // What exactly is happening here?
  for (let i = x; i--; i >= 1) {
    result *= x;
  }
  return x;
}

/**
 * Recursive style
 */
function factorialB(x) {
  if (x === 0) {
    return 1;
  }
  // Recursive call (function calls itself!)
  // Stays true to definition of factorial: x times the factorial of x - 1
  return x * factorial(x - 1);
}

/**
 * Imperative style
 */
function fibonacciA(n) {
  // Term 0: 1, Term 1: 1, Term 2: 2
  n = n - 1;
  let prevTerm = 1;
  let currTerm = 1;
  // What does this loop do, exactly?
  for (let i = 0; i < n; i += 1) {
    let temp = prevTerm;
    prevTerm = currTerm;
    currTerm += temp;
  }
  return currTerm;
}

/**
 * Recursive style
 */
function fibonacciB(n) {
  if (n === 0 || n === 1) {
    return 1;
  }
  // Definition of next Fibonacci term is sum of two previous
  // Easy to follow!
  return fibonacci(n - 2) + fibonacci(n - 1);
}

Many high-level languages, JavaScript included, support recursion. But some languages don't, and in the field of theoretical computer science, introducing recursion into non-recursive contexts is a fascinating problem.

This is where the Y combinator comes in: it provides a way to recurse — to self-reference — even if self-reference is unsupported in the base language!

Eliminating Recursion

The Y combinator bestows the power of self-referential recursion unto languages which don't support it. So to derive it in JavaScript, let's pretend a little — let's pretend that JavaScript doesn't support recursion.

I've put the recursive factorial function given in the initial examples in the block below. If everything goes well, by the end of this writeup we'll have a tool that will allow this factorial function to self-reference again — but most importantly, without any self-reference in the function itself!

function factorial(x) {
  if (x === 0) {
    return 1;
  }
  return x * factorial(x - 1);
}

The best way to begin removing the recursion from factorial looks like factoring out the call to factorial from the function body and making it a parameter, so let's do that.

Bringing Our Own

// Bring your own factorial function!
function byoFactorial(f, x) {
  if (x === 0) {
    return 1;
  }
  return x * f(x - 1);
}

With this new factorial function, byoFactorial, we have to "bring our own" working factorial function f to pass into the new, non-recursive function as a parameter, to replace our old self-referential call.

Of course, the problem now is that we don't have a working factorial function anymore. But that doesn't mean we have to give up! We can start small — from zero.

Let's begin by creating a function f, that when passed to byoFactorial, will make it work, but only for x = 0 (0! = 1).

0! is defined to be equal to 1 — but why? It comes from combinatorics, the study of counting and choosing. In combinatorics, the definition of n! is the number of orders and ways n items can be chosen (i.e. permutations).

For instance, 2! = 2 is the number of ways you can select and order two items — the first item, then the second; or the second item, then the first. By that same token, 0! is the number of ways you can select and order zero items — and you can do that in only 1 way.

How can we create this function f for which byoFactorial will work for x = 0 (0! = 1)? Well, closer inspection of our byoFactorial function shows that it already has a base case defined — when x is 0, it returns 1. Moreover, when x = 0, no self-reference occured anyway in the original factorial function — thus, f is not called.

That means we can pass any arbitrary function as f. When x = 0, byoFactorial will still return 1 regardless.

Here are some suggestions.

function identity(x) {
  return x;
}
function one(x) {
  return 1;
}
function random(x) {
  return Math.random();
}
// I like to use `random` because you'll
// immediately know if your function stops
// working - you'll get a long and ugly
// decimal. With the `identity` or `one` functions,
// problems with output are more likely to slip
// through. For the rest of this writeup, I'll
// use `random`.

byoFactorial(random, 0);
// => 1 - it works!
byoFactorial(random, 1);
// => 0.07382473983422022

So far, we've been passing a function f to byoFactorial, but we can just as easily create replacement factorial functions from byoFactorial by binding f. Using this method, we'll create new functions which we can call with just one parameter — our desired factorial, x.

In our case, bind takes two parameters: a this value and then the actual first parameter for byoFactorial, f. Since the body of byoFactorial doesn't access this at all, we can just set it to null.

function byoFactorial(f, x) {
  if (x === 0) {
    return 1;
  }
  return x * f(x - 1);
}

// Pass null because there's nothing specific we need to set `this` to
const factorialUpTo0 = byoFactorial.bind(null, Math.random);
// factorialUpTo0 will work with x = 0, and can be called like a regular function:
factorialUpTo0(0);
// => 1

Here's what we get:

  factorialUpTo0(0) => 1
  // I passed Math.random as the first parameter so you'll probably get different results
  factorialUpTo0(1) => 0.07382473983422022
  factorialUpTo0(2) => 0.7045168327647198
  factorialUpTo0(3) => 1.4614935135773812
  factorialUpTo0(4) => 0.3311529571140488

As expected, it works for 0!, but nothing else. But it's progress! We're 1/infinity done our complete factorial function!

1/infinity is bigger than you think! Ever wondered what the sum of 1/2 + 1/3 + 1/4 ... + 1/infinity + 1/(infinity + 1) was? Yep, it's infinity.

function byoFactorial(f, x) {
  if (x === 0) {
    return 1;
  }
  return x * f(x - 1);
}

Let's make byoFactorial work for both 0! and 1!. In other words, how can we create a function f that we can bind to byoFactorial that'll allow it to return correct outputs for x = 0 and x = 1?

First, let's walk through what happens when we pass x = 1 into byoFactorial. For whatever f we come up with, byoFactorial(f, 1) will return 1 * f(0). So, all we need is a factorial function f which returns the correct value for the case when x = 0. Do we already have a factorial function which works for 0!?

We do, and it's called factorialUpTo0! Let's bind it to byoFactorial. This will create a factorial function which will work for both x = 0 and 1 — or rather, all integer values from 0 up to 1 (this process will be easier to reason about if we think about it this way). We'll call this function factorialUpTo1.

const factorialUpTo1 = byoFactorial.bind(null, factorialUpTo0);

Before we keep going, let's refactor our byoFactorial function. Calling .bind is clunky (especially with that null!) and we can clean up our syntax by returning a function instead (in essence, creating a "factory").

function factorialFactory(f) {
  return function factorial(x) {
    if (x === 0) {
      return 1;
    }
    return x * f(x - 1);
  };
}

Now, we can create factorialUpTo0 and factorialUpTo1 functions with much cleaner syntax.

const factorialUpTo0 = factorialFactory(Math.random);
const factorialUpTo1 = factorialFactory(factorialUpTo0);
// Instead of
// const factorialUpTo1 = byoFactorial.bind(null, factorialUpTo0);

And we can make factorialUpTo2, too!

const factorialUpTo2 = factorialFactory(factorialUpTo1);

factorialUpTo2 will work with for x = 2, because it will return 2 * factorialUpTo1(1), and we already know that factorialUpTo1 will work up to 1, so we also know that factorialUpTo2 will return correct outputs for all values up to 1 as well!

const factorialUpTo3 = factorialFactory(factorialUpTo2);

By the same token, factorialUpTo3 will work for 3!, because it will return 3 * factorialUpTo2(2), and we already know that factorialUpTo2 will work on all values up to 2!

We can continue this pattern to create our complete, working, non-recursive factorial function.

const factorialUpTo3 = factorialFactory(factorialUpTo2);
const factorialUpTo4 = factorialFactory(factorialUpTo3);
const factorialUpTo5 = factorialFactory(factorialUpTo4);
const factorialUpTo6 = factorialFactory(factorialUpTo5);
const factorialUpTo7 = factorialFactory(factorialUpTo6);
const factorialUpTo8 = factorialFactory(factorialUpTo7);
const factorialUpTo9 = factorialFactory(factorialUpTo8);
const factorialUpTo10 = factorialFactory(factorialUpTo9);
// ...
factorialUpTo10(5);
// => 120
factorialUpTo10(8);
// => 40320
factorialUpTo10(10);
// => 3628800
factorialUpTo10(11);
// => 28570479.681626465
factorialUpTo10(12);
// => 79140708.41594502

Note that the very first function f we passed to factorialFactory to create factorialUpTo0 (in my case, Math.random) is only called if we pass an x greater than the upper bound of our factorialUpTo{x} function. If we keep passing our newly created factorialUpTo{x} functions back into factorialFactory, ad infinitum, Math.random will never be called (because the upper bound will be at infinity), and our function will work over all values of x!

Here's what factorialUpTo10 looks like, expanded.

const factorialUpTo10 = factorialFactory(
  factorialFactory(
    factorialFactory(
      factorialFactory(
        factorialFactory(
          factorialFactory(
            factorialFactory(
              factorialFactory(
                factorialFactory(
                  factorialFactory(factorialFactory(Math.random))
                )
              )
            )
          )
        )
      )
    )
  )
);

So, it looks like we'll need to apply factorialFactory to itself ad infinitum to get our working factorial function. How can we do that though?

const factorialUpToInfinity = ???

Here Comes Y!

The Y combinator is here to save the day! The Y combinator is a function which applies another function infinite times, and in simple terms can be defined like below.

function y(f) {
  return f(f(f(f(f(f(f(f(f(f(f(f(f(...)))))))))))));
}

Unfortunately, JavaScript can't evaluate the above expression. We need to simplify it — and to start, it helps to think about the definition of y in the context of infinite sums.

A Math Problem

What's the sum of sqrt(2 + sqrt(2 + sqrt(2 + sqrt(2 + sqrt(2 ...)))))?

The solution is simple. Let's call the sum S, so S = sqrt(2 + sqrt(2 + sqrt(2 + sqrt(2 + sqrt(2 ...))))).

Now, if we look closely at the expression, we can see S is a part of itself! The sum can alternatively be written as S = sqrt(2 + S).

Squaring both sides, we get S^2 = S + 2. Moving all terms of S to the left side, we get S^2 - S - 2 = 0. Factored, this is (S - 2)(S + 1) = 0, so the two solutions to this equation are S = -1 and S = 2. Since sqrt returns the principal (non-negative) square root, our solution must be S = 2.

We can apply this same principle to our original formulation of the Y-combinator: y(f) = f(f(f(f(f(f(f(f(f(f(f(f(f(...))))))))))))). Looking closely, it's clear that y(f) is a part of the equation for y(f)! We can write the new equation for y(f) like so: y(f) = f(y(f)).

We can wrap that expression in another function so we can explicitly pass our x parameter, too.

function y(f) {
  return function(x) {
    return f(y(f))(x);
  };
}

There's another reason we can't define our version of y as simply y(f) = f(y(f)).

function y(f) {
  return f(y(f));
}

When we evaluate the above, we get this:

const tenFactorial = y(factorialFactory)(10);
// => RangeError: Maximum call stack size exceeded

The problem is that JavaScript tries to evaluate y(factorialFactory), which never finishes, before doing any computation. Let's quickly walk through the evaluation.

function y(f) {
  return f(y(f));
}

y(factorialFactory)(10);
factorialFactory(y(factorialFactory))(10);
factorialFactory(factorialFactory(y(factorialFactory)))(10);

This continues until we get the stack overflow error.

On the other hand, when we wrap the expression in an outer function to pass the parameter x, we also defer evaluation of y(f). The term for this type of outer function is a "thunk", which you may have heard from libraries like redux-thunk, which does the same thing but for Redux, a popular state management library often paired with React.

function y(f) {
  return function thunk(x) {
    return f(y(f))(x);
  };
}

Let's walk through the thunked evaluation.

function factorialFactory(f) {
  return function factorial(x) {
    if (x === 0) {
      return 1;
    }
    return x * f(x - 1);
  };
}

y(factorialFactory)(10)

thunk(10) {
  return factorialFactory(y(factorialFactory))(10)
}

factorialFactory(y(factorialFactory))(10)

factorialFactory(function thunk(x) {
  return factorialFactory(y(factorialFactory))(x)
})(10)

// At this point, the first argument to factorialFactory
// has been fully evaluated (the thunk is the result of
// the evalation)! Now, the body of factorialFactory can
// actually be run.

10 * (function thunk(x) {
  return factorialFactory(y(factorialFactory))(x);
})(9)

10 * factorialFactory(y(factorialFactory))(9);

// And so on

The evaluation semantics of JavaScript are really the only thing preventing us from defining the Y combinator as we had it originally (y(f) = f(y(f))). In other languages, it's completely acceptable!

In Haskell, a functional language, the Y combinator can be defined as we did above initially: y(f) = f(y(f)). The reason this is possible is because Haskell's evaluation semantics are different — Haskell is a lazy language. By default, it doesn't fully evaluate expressions until they are truly needed.

Here's how Haskell would evaluate y(factorialFactory)(10) above, given that y was defined as we had it originally.

// Our factorialFactory, in JavaScript for reference
function factorialFactory(f) {
  return function factorial(x) {
    if (x === 0) {
      return 1;
    }
    return x * f(x - 1);
  };
}

y(factorialFactory)(10)
# Haskell will initially unpack the call to y by one layer
factorialFactory(y(factorialFactory))(10)
# At this point, Haskell will look at the call to factorialFactory, instead of continuing to unpack the original y (which is what JavaScript does)
return 10 * y(factorialFactory)(9)
# Haskell will repeat the above process for the rest of the calls to y
# ...
return 10 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1 * factorialFactory(y(factorialFactory))(0)
# At this point, factorialFactory encounters its base case and returns 1
# Haskell never computes the actual value of y(f)!

But There's Still Recursion!

Our current definition y of the Y combinator still contains recursion, though! One of the main selling points of the Y combinator is that it allows us to add support for recursion to languages which don't support it — so there must be a way to get rid of the recursive call.

function y(f) {
  return function thunk(x) {
    return f(y(f))(x);
  };
}

We could take the same approach as we did before, factoring out the recursive call into a parameter and creating a "factory" function, but that won't fly — as we saw in the factorial example, we'd still need to apply that factory function ad infinitum to create a functional y.

Let's take a closer look at y, then. How can we define y in non-recursive terms? Well, we can take advantage of the fact that while we are voluntarily shunning self-reference in function bodies, we can still pass functions to themselves as parameters!

We'll need to make a clever substitution, though. Instead of defining y(f) as we have it now, let's define it as y(f) = x(x)(f), for some other function x. In simpler terms, y = x(x) — y is x applied to itself.

// Here's our current, recursively-defined y
function y(f) {
  return function thunk(n) {
    return f(y(f))(n);
  };
}

// Apply the substitution y = x(x)
// Call the parameter otherX since we don't want
// to confuse the outer x and inner x and to avoid
// variable shadowing
function x(otherX) {
  return function y(f) {
    return function thunk(n) {
      return f(otherX(otherX)(f))(n);
    };
  };
}

Let's try this out.

const newY = x(x);

// x(x)(factorialFactory)
const newFactorial = newY(factorialFactory);

newFactorial(10);
// => 3628800

It works! Let's walk through the evaluation.

function x(otherX) {
  return function y(f) {
    return function thunk(n) {
      return f(otherX(otherX)(f))(n);
    };
  };
}

x(x)(f);

return function thunk(n) {
  return f(x(x)(f))(n);
};

// Unthunked
f(x(x)(f));

// From first step above, we see that x(x)(f) = f(x(x)(f))
// We can apply this substitution
f(f(x(x)(f)));

// And again, and again... look familiar?
f(f(f(f(f(f(x(x)(f)))))));

It works! By applying x to itself, we avoid self-reference in the function body. Everything the function needs to run comes from its parameters.

And with a little bit more refactoring and substitution, we've got the non-recursive Y combinator!

// What we already have
function x(otherX) {
  return function y(f) {
    return function thunk(n) {
      // By passing `x` to itself (in the form of `otherX`),
      // we can technically "call" `x` inside the function
      // body of `x` - but importantly, non-recursively! Of course,
      // now that we've altered the parameters of `x` to take
      // itself, we need to pass `otherX` to `otherX` in the
      // return statement, too.
      return f(otherX(otherX)(f))(n);
    };
  };
}

// Let's refactor
const y = x(x);

// Here's `x` agian
function x(otherX) {
  return function y(f) {
    return function thunk(n) {
      return f(otherX(otherX)(f))(n);
    };
  };
}

// Now, just substitute the body of `x`
// for each `x` in the statement `y = x(x)`
const y = (function(otherX) {
  return function(f) {
    return function thunk(n) {
      return f(otherX(otherX)(f))(n);
    };
  };
})(function(otherX) {
  return function(f) {
    return function thunk(n) {
      return f(otherX(otherX)(f))(n);
    };
  };
});

// If we want `y` to be usable on functions
// with any number of arguments, we can use
// the ES6 spread syntax over the arguments
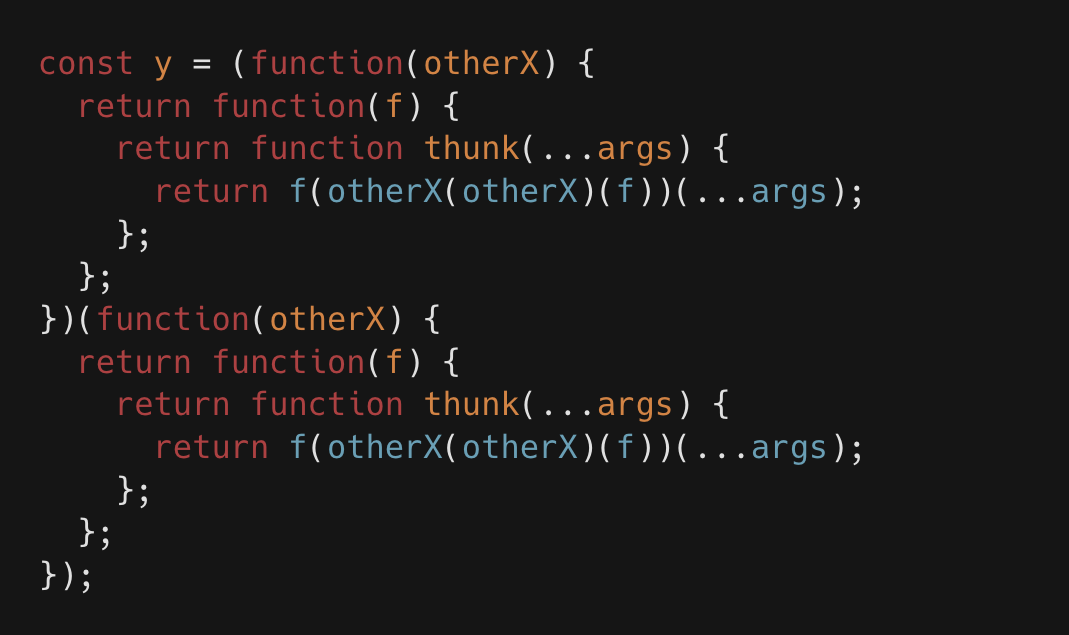
const y = (function(otherX) {
  return function(f) {
    return function thunk(...args) {
      return f(otherX(otherX)(f))(...args);
    };
  };
})(function(otherX) {
  return function(f) {
    return function thunk(...args) {
      return f(otherX(otherX)(f))(...args);
    };
  };
});

// We can shorten it even more with ES6 arrow functions
const y = (x => f => (...a) => f(x(x)(f))(...a))(x => f => (...a) =>
  f(x(x)(f))(...a)
);

And there you go! One of the most important concepts in theoretical computer science, sitting on your lap in just a few characters.

const y = (x => f => (...a) => f(x(x)(f))(...a))(x => f => (...a) =>
  f(x(x)(f))(...a)
);

Appendix

Try writing your own y-compatible, non-recursive implementations of your favorite recursive processes! Here's an example with the Fibonacci sequence mentioned earlier.

function fibonacciFactory(f) {
  return function thunk(n) {
    if (n === 0 || n === 1) {
      return 1;
    }
    return f(n - 2) + f(n - 1);
  };
}

const fibonacci = y(fibonacciFactory);
fibonacci(10);
// => 89

About the Author

Thanks for reading! My name is Nathan Leung. I'm the founder of location-based social messaging app Suap and an incoming first-year student at the University of Michigan.

You can learn more about me on my LinkedIn or on my personal website, and I encourage you to try Suap at getsuap.com!